MFCC Speaker Recognition
Speaker Recognition model based on Mel Frequency Cepstral Coefficients
This project is an approach we used for our solution at Signal Processing Cup 2024. Full solution code by Team Eigensharks can be found here.
Robovox Challenge - SP Sup 2024
The primary task of Signal Processing Cup 2024 was Far-Field Speaker Recognition by a Mobile Robot. During this task we had to accurately classify noisy audio recordings of 71 speakers. Our solution contain mainly two steps; denoising the audio files and classification. After denoising and preprocessing stages (using Wavelet transform etc.), we used several deep learning techniques and models to create a speaker embedding.
Read more about the competition here.
About the Dataset
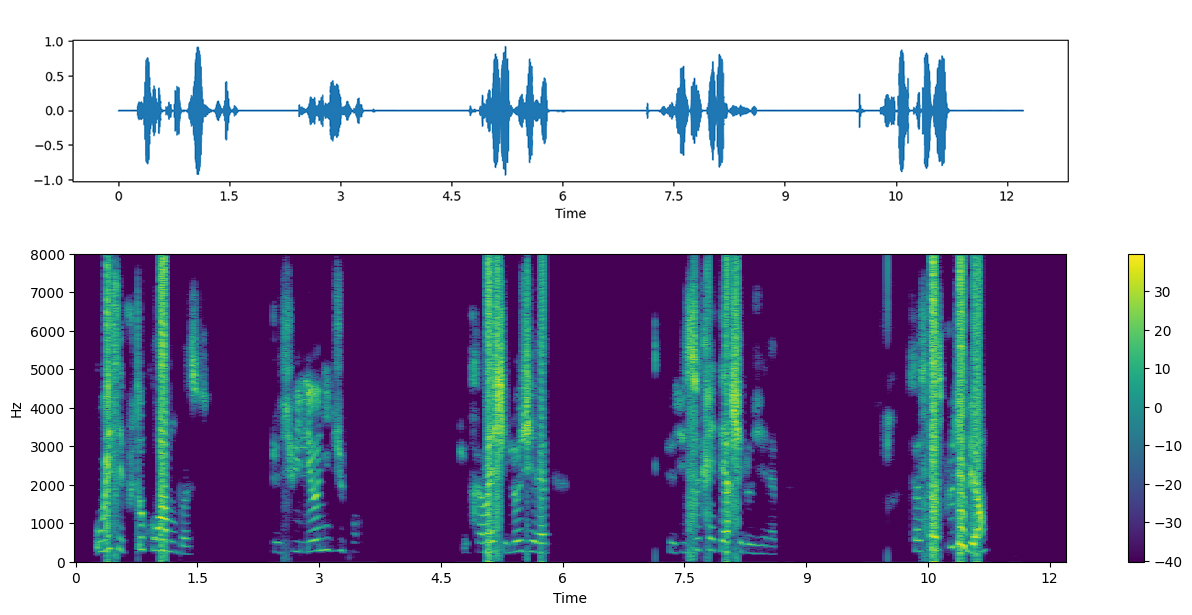
The Robovox dataset features recordings from a mobile robot equipped with speaker recognition capabilities, utilizing a loudspeaker located beneath it to communicate. With contributions from 78 speakers, the dataset comprises approximately 11,000 recorded dialogues, generated through 2,219 conversations, each typically consisting of 5 speaker turns. These recordings, averaging 3.6 seconds in length, are captured in various acoustic settings and are available in 8-channel format.
MFCC + Deep Learning approach
One approach of our solution applied the technique of extracting MFCC from the audio samples and feeding them into a Deep Neural Network (DNN) for training. When a feature extractor of an speech audio sample (such as STFT or MFCC) is fed into a DNN model, it learns to create a feature space, known as an embedding, from several such samples of audio. That is, when given a unique voice recording of a speaker, the model maps it to a certain point on a feature space (similar to a vector space) unique to that speaker. We can force the model to map recordings of similar voices to the same point, by selecting an appropriate loss function. During our implementation we architectured a popular DNN structure known as a bidirectional LSTM with Triplet Cosine Loss as the loss function. This loss function relies on cosine distance, a popular metric of similarity in a vector embedding context. Using the speaker embedding we formulated using this approach, we were able to inference accurately on new data, to classify which speaker each recording belonged to.
Read more about MFCCs here.
Mel-Frequency Cepstral Coefficients
It was discovered that by analyzing the spectrum of a spectrum (Known as the cepstrum), the periodic structures within the frequency spectrum can be revealed, offering insights into the low-frequency periodic vibrations from vocal cords and the formant filtering effects in the larynx. Cepstral coefficients can be calculated as follows,
\[C_p = |\mathcal{F}\{log(|\mathcal{F}\{f(t)\}|^2)\}|^2\]By adopting the Mel-scale during log-scaling stage, improves sensitivity to human voice. By employing the Mel-frequency cepstrum, derived from scaling spectrum coefficients with the Mel-scale, a more accurate representation of vocal characteristics can be achieved. The calculation process involves utilizing a triangular filter-bank and various technical considerations, but it can be calculated in one line of code in Python using Librosa library.
import librosa
import librosa.display
# Load audio waveform
x, sr = librosa.load("audio.wav", sr=None)
# Calculate MFCC spectrum
mfccs = librosa.feature.mfcc(y=x, sr=sr, n_mfcc=40)
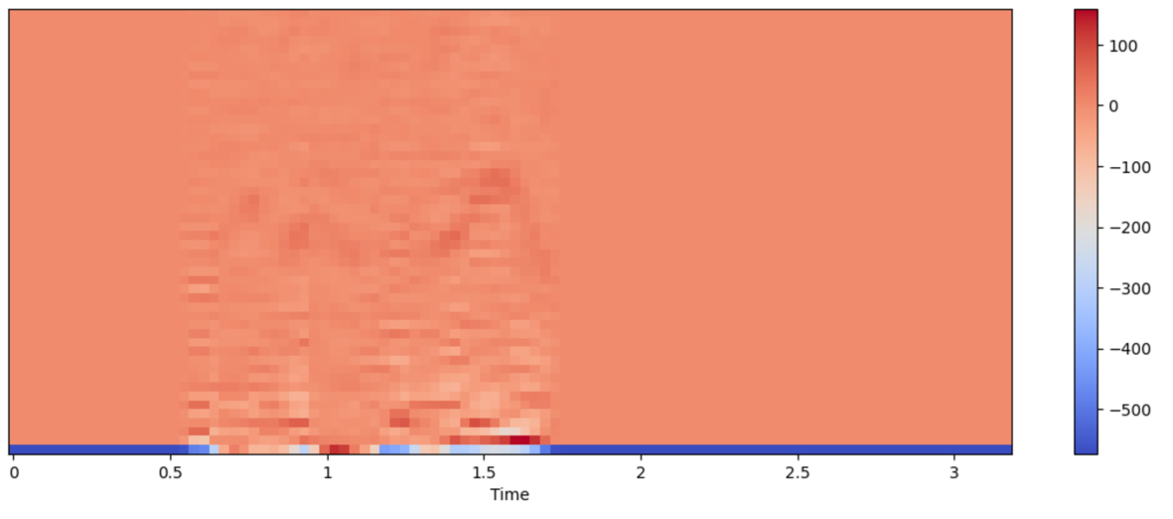
MFCC obtained for one example recording as such is shown below.
File Structure
-
model.pycontains the code for LSTM model. -
loss.pycontains the Triplet Cosine Loss funtion definition. -
feature_extraction.pycontains the helper function code to obtian MFCC coefficients during feature extraction. -
data.pycontains the code for structuring, preprocessing and loading the ROBOVOX dataset. -
train.pycontains the code for training the model. -
visualize_data.ipynbis a Jupyter Notebook which explores the dataset by observing STFT, MFCC and other features of the audio data.
Technologies used
- PyTorch
- Librosa
- Google Colab
Other
Full solution code: https://github.com/eigensharks/Eigensharks